- 貨架第三方檢測-CNAS/CMA/SEMA三重資質認可認定
- phone021-67157048
- recent_actors
職業責任險 - bubble_chart
產品責任險 - security
公正性聲明 - gavel
侵權聲明
- event2021-11-20 13:40:51
- person 穩圖WESAFE
- local_library 原創
- visibility 閱讀:463
構件設計承載力應通過測試或理論計算方法確定。理論計算方法應合理考慮開孔與局部屈曲、整體屈曲和畸變屈曲以及缺陷的相互作用影響。對于連續開孔的構件,理論計算方法應通過測試驗證。
連續開孔構件的設計需要測試,但是并不限制理論計算方法(比如有限元法)應用于開孔或無孔構件的計算。
一、截面特性
計算截面特性時,毛截面面積應在展開鋼帶名義截面面積的±2%以內。
1.1剛度
開孔對剛度(或變形)的影響可通過相關測試方法確定,亦可以通過有限元或等效截面計算。
為了簡化計算,開孔可假定為矩形(見圖1與圖2)。
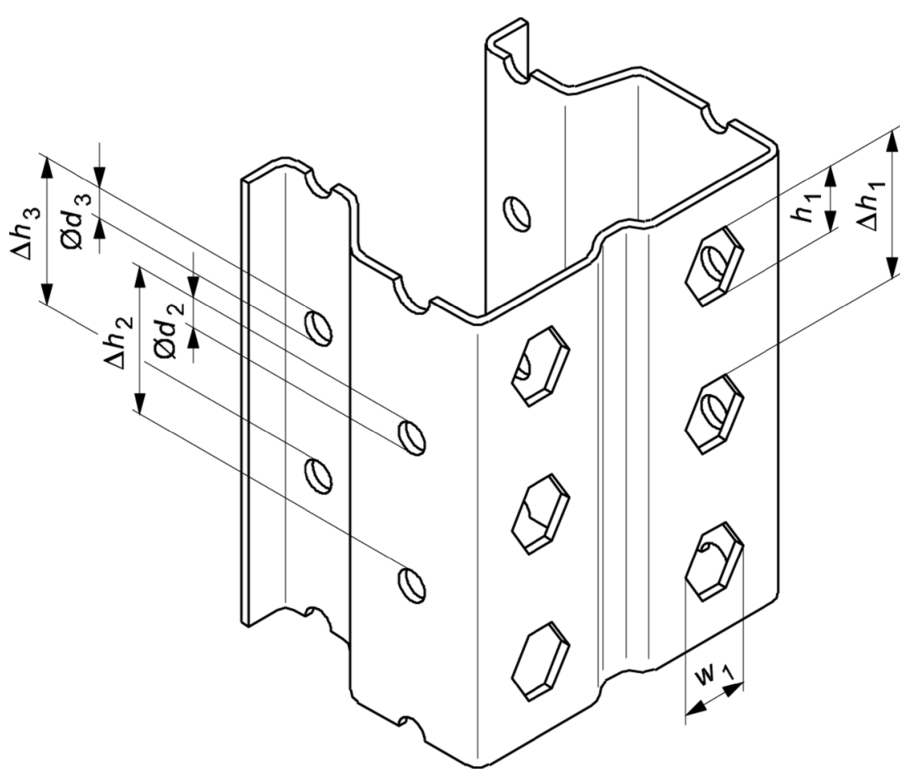
圖1 原始截面形狀
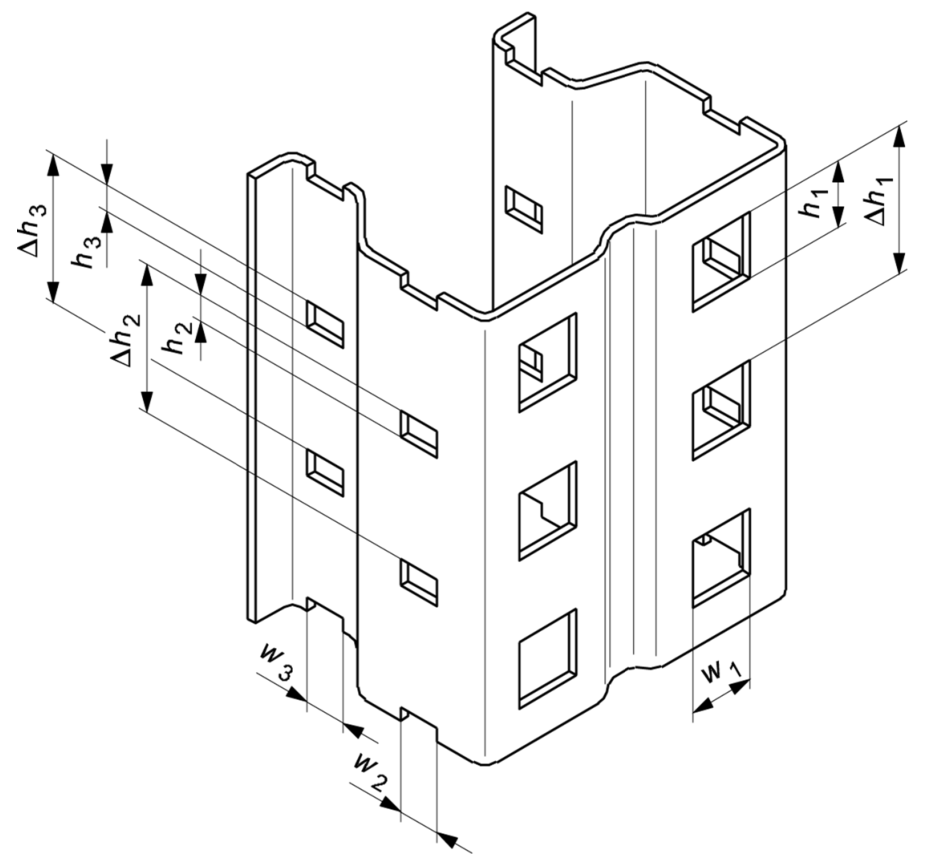
圖2 簡化成矩形孔后的截面形狀
開孔效應由截面局部厚度的折減表示,截面被劃分為不同厚度的板條(見圖3)。
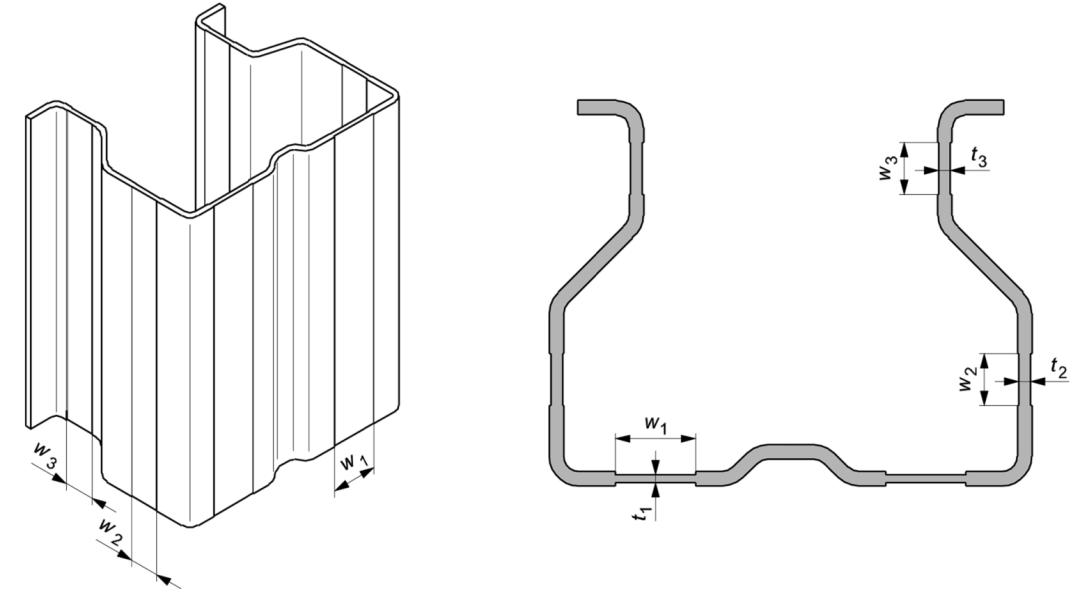
圖3 等效厚度板條的截面
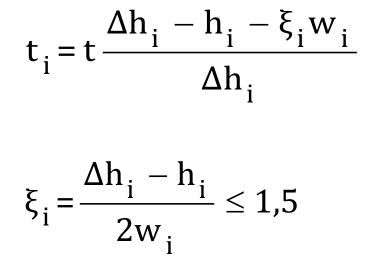
其中,
ti為板條等效厚度;
t為截面名義厚度;
Δhi為孔間距;
Hi、di為孔的高度;
wi為孔的寬度;
ξi為開孔影響系數。
等效截面的特性可用合適的軟件或公式計算。
計算剛度的相關等效截面特性有:
——截面積Aeq
——強軸慣性矩Iy,eq
——弱軸慣性矩Iz,eq
——扭轉常數IT,eq
——翹曲常數Iw,eq
可將凈截面特性作為等效截面特性。
1.2 強度
相關有效截面特性有:
——截面積Aeff
——強軸截面模量Weff,y
——弱軸截面模量Weff,z
二、橫梁的設計
受彎構件承載力應考慮彎曲、軸壓與剪切作用,通過相關測試或理論方法計算確定,如有需要還應考慮:
a)局部屈曲;
b)腹板壓屈;
c)側向扭轉屈曲;
d)非彈性行為;
e)翼緣翹曲;
f)扭轉;
g)構件缺陷。
2.1 側向扭轉屈曲不起控制作用的橫梁
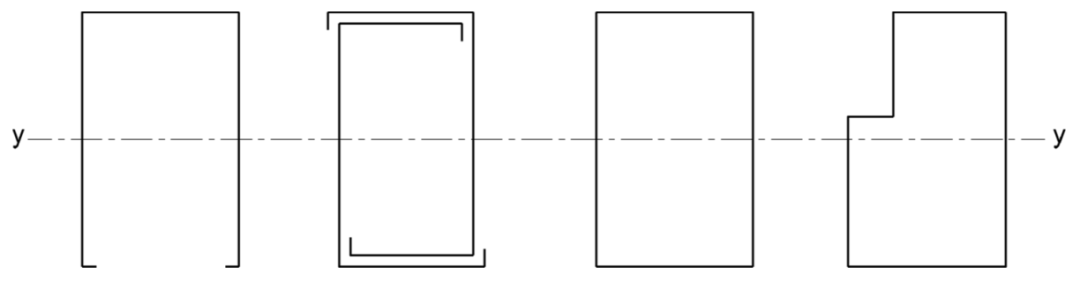
圖4 側向扭轉屈曲不起控制作用的橫梁截面示例
當橫梁跨度很大時,圖4截面的橫梁也可能會發生側向扭轉屈曲。圖5給出了箱型截面橫梁側向扭轉屈曲不起控制作用的(截面高度)/(截面寬度)近似限值。
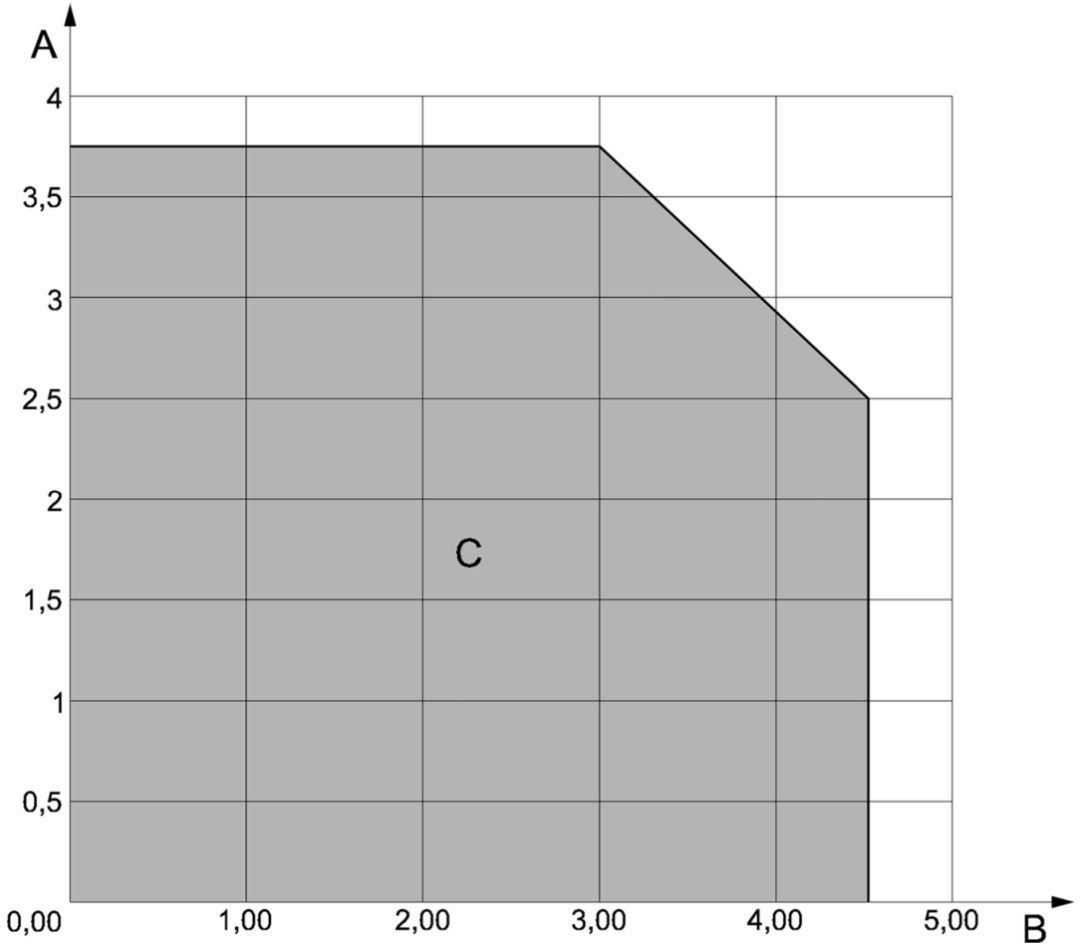
A 橫梁截面長細率,即高寬比
B 橫梁跨度,單位m
C 側向扭轉屈曲不起控制作用的區域
圖5 橫梁側向扭轉屈曲無需考慮的長細率范圍
對于側向扭轉屈曲不起控制作用的受彎構件,彎曲承載力應根據相關標準計算。左右對稱放置貨載的橫梁近似設計方法如下(該近似方法已經編成了對應小程序):識別下方二維碼關注公眾號即可進入小程序
穩圖貨架橫梁承載力校核計算橫梁承載力校核計算小程序
2.1.1 跨中彎矩
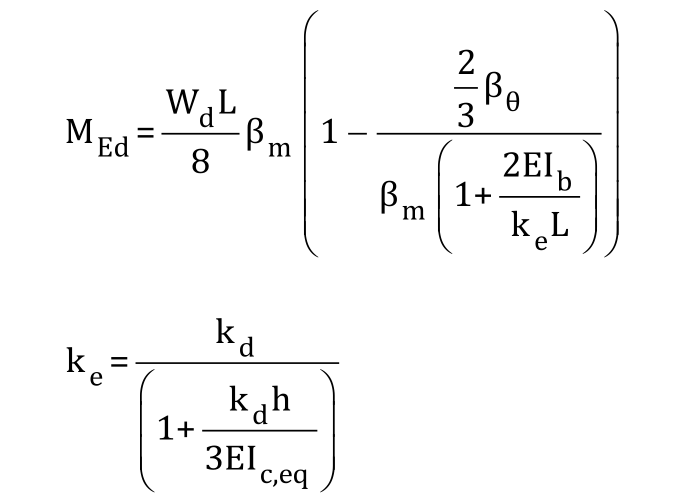
其中
Wd為單根橫梁承受荷載的設計值;
L為橫梁凈跨(立柱邊到邊);
h為層高;
kd為梁柱節點剛度;
Ib為橫梁慣性矩;
Ic,eq為立柱強軸慣性矩。
βθ和βm見表1。
2.1.2 撓度
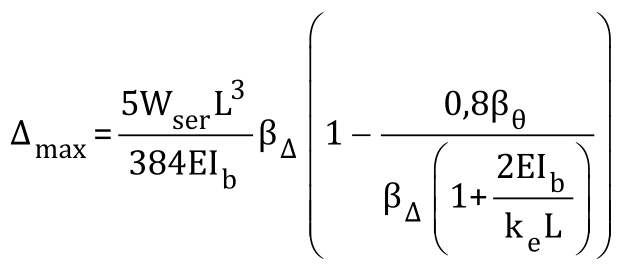
其中
Wser為單根橫梁承受荷載的標準值;
βθ和βΔ見表1。
以上計算式基于的模型見圖6。
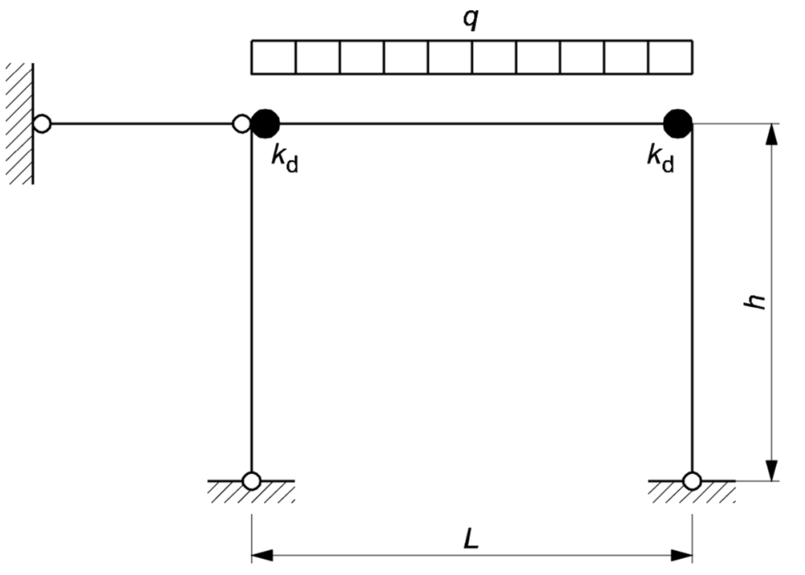
圖6 橫梁近似計算模型
2.1.3 等效橫梁荷載
對于橫梁上荷載不是均布荷載的情況,應根據表1中的系數將實際荷載布置轉化成等效均布荷載。
表1 橫梁荷載系數
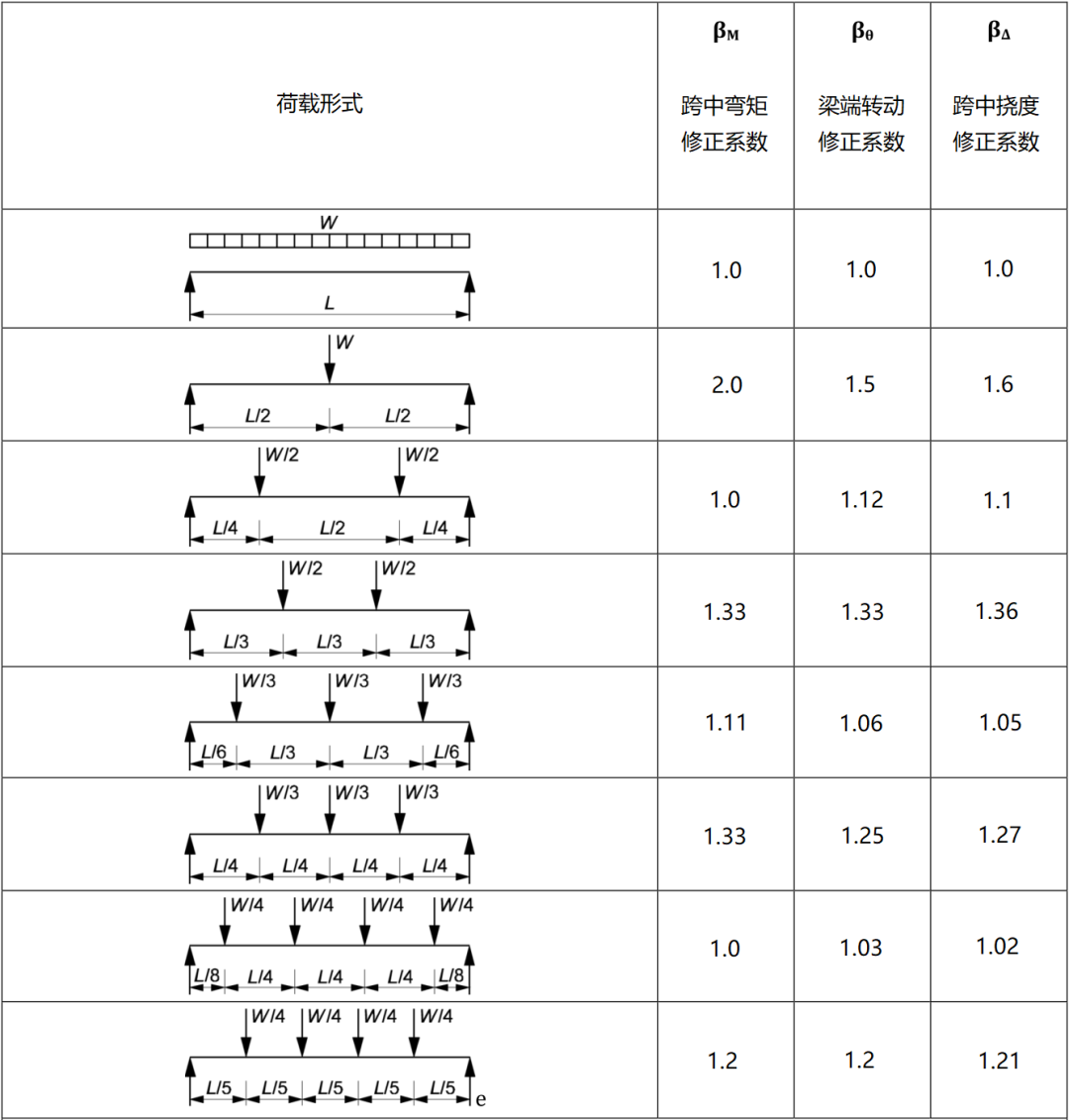
2.2 側向扭轉屈曲的橫梁
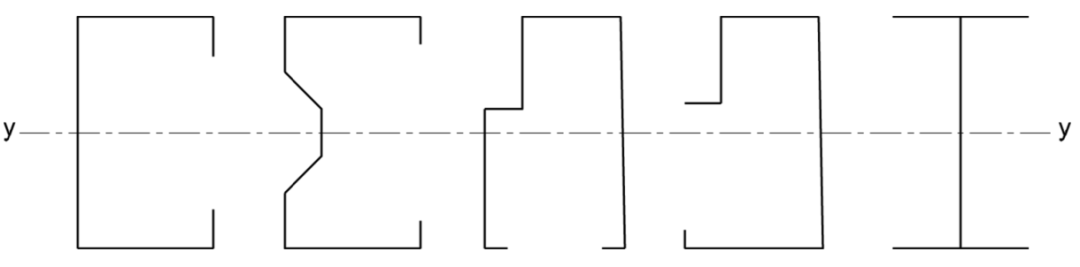
圖7 側向扭轉屈曲起控制作用的橫梁截面示例
開口截面的貨架橫梁,受彎平面不是對稱軸平面,受彎的同時受扭,特別易發生側向屈曲。雖然受到貨物托盤部分程度的約束,但是其強度與剛度最好通過測試確定。C型抱焊梁強度取決于一系列參數,如截面高寬比、C型截面抱扣的程度、C型截面卷邊寬度、是否有點焊及點焊間距等。
在正常的放貨卸貨條件下應確保橫梁的扭轉穩定性。
橫梁側向扭轉屈曲強度Mb,Rd應進行測試或以下方法計算確定:
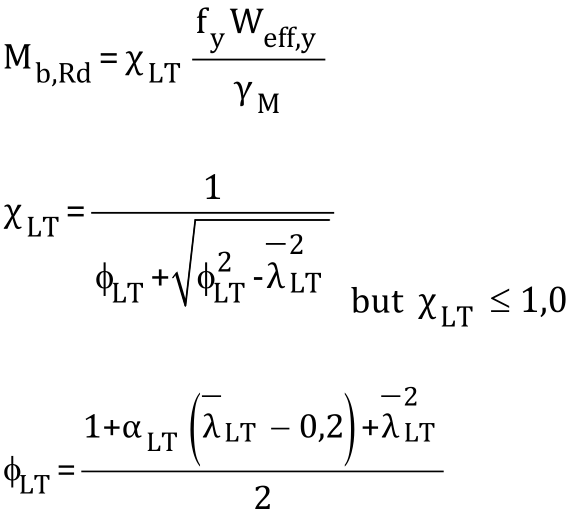
其中
fy為鋼材屈服強度特征值;
Weff,y為強軸有效截面模量。
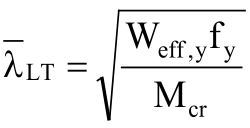
αLT=0.34(一般截面)
αLT=0.49(開口冷成型截面,如∑形截面)
Mcr的計算應基于毛截面特性,有效長度取橫梁長度。
2.3 存儲單元與橫梁的相互作用
2.3.1 確定彎矩
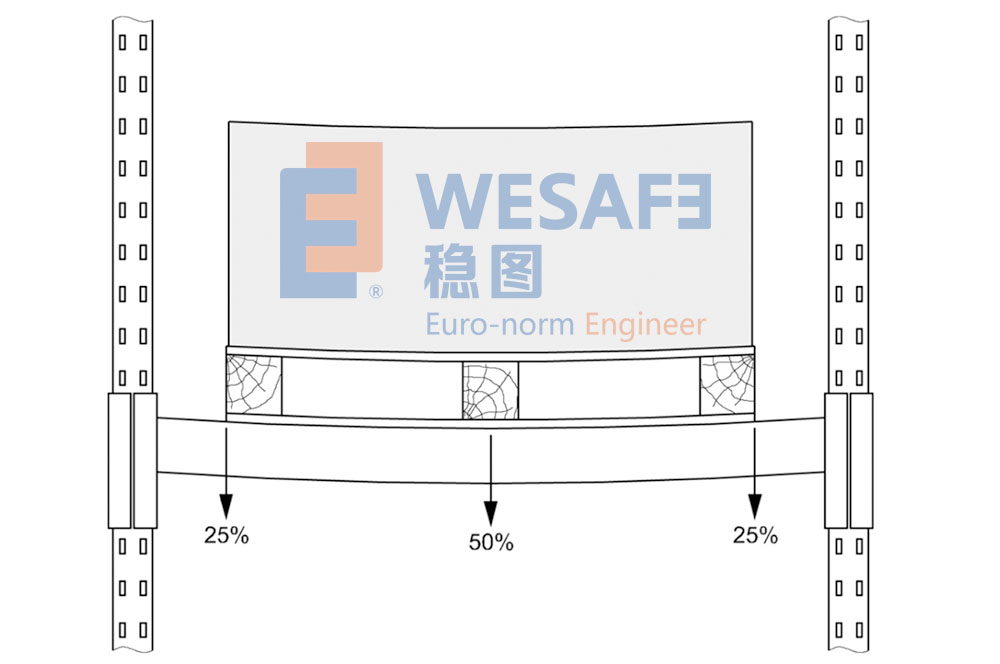
一般認為當每組橫梁上存儲單元數目多于一個時,可認為橫梁上的荷載為均勻分布。對于僅有一個存儲單元的情況,應認為橫梁上的荷載分布如圖8所示。
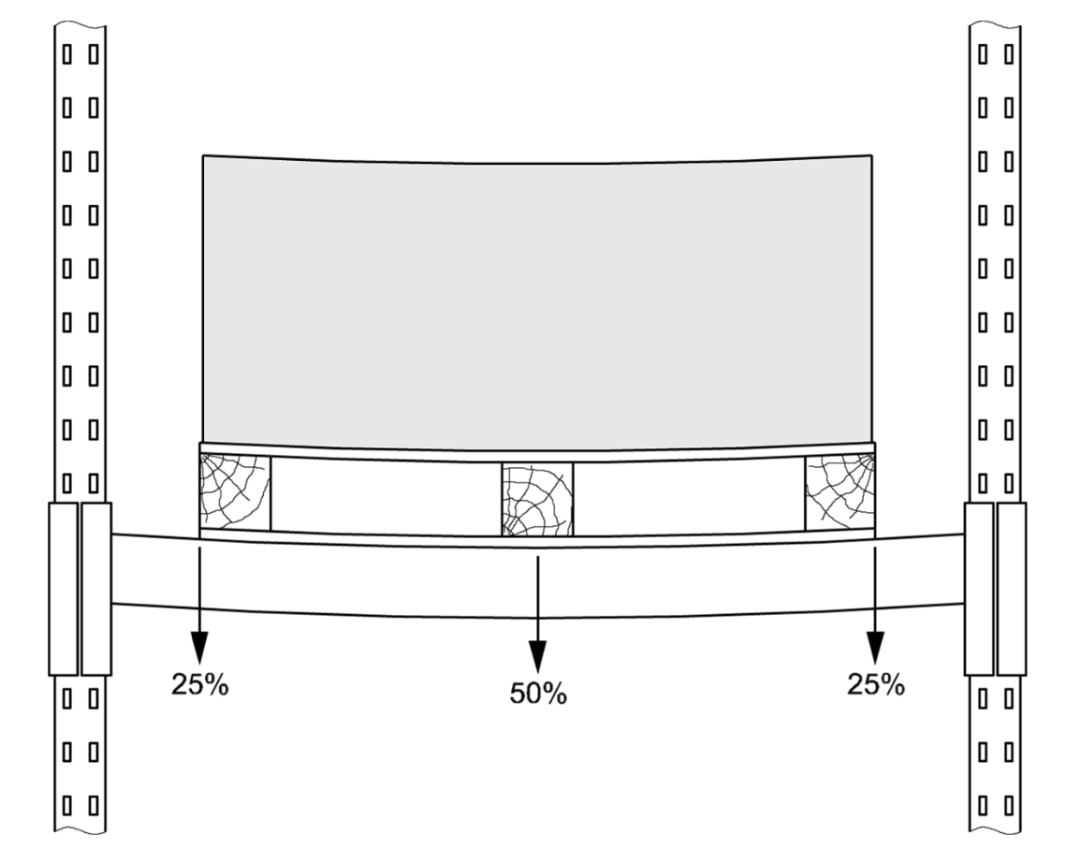
圖8 荷載分配
2.3.2 腹板壓屈
當校核橫梁的腹板壓屈或腹板壓屈與彎曲組合時,保守假定所有荷載通過托盤最外兩側的構件施加于橫梁,見圖9。
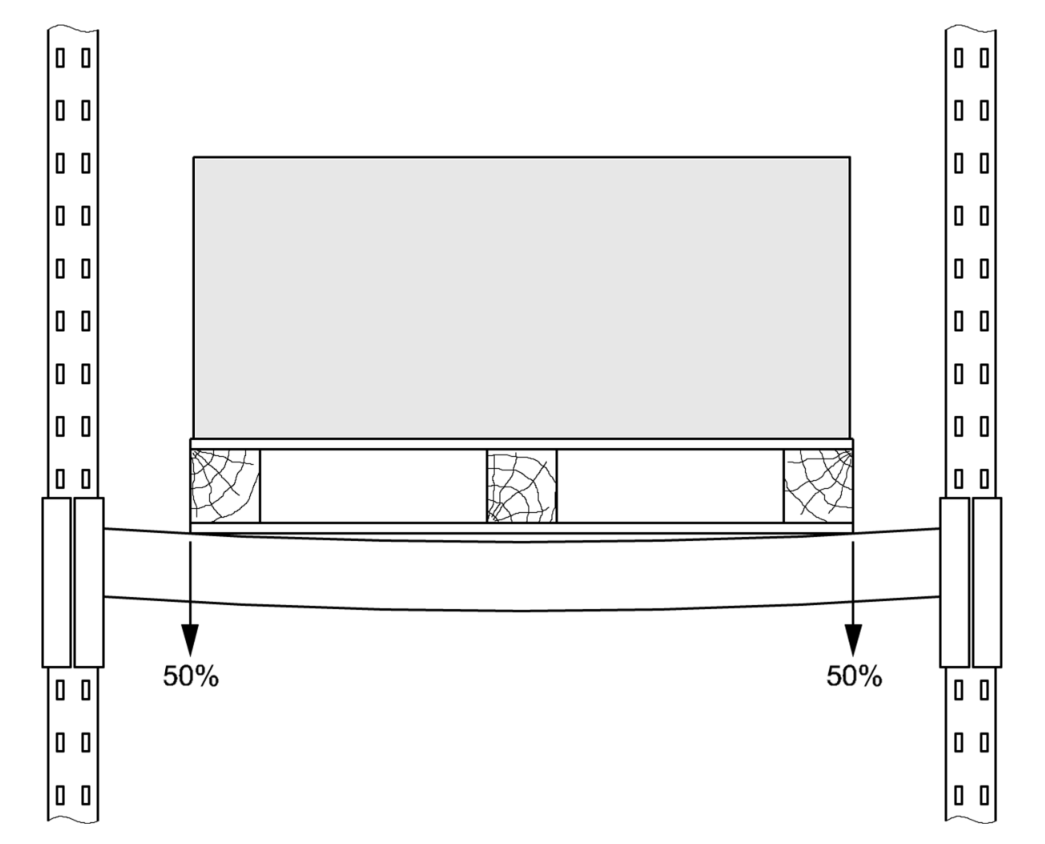
圖9 腹板壓屈荷載分配
2.3.3 特殊情況
設計人員應確定可能導致橫梁較高應力的特殊存儲狀況。例如,輪胎或桶狀容器會在施加豎向荷載的同時施加水平荷載、使用較窄的托盤會導致荷載易向橫梁跨中集中等。
2.4 塑性設計
橫梁可進行塑性設計,前提是恰當考慮梁柱節點的轉動能力及其對結構整體變形的影響。
2.5 受到壓彎作用的橫梁
當橫梁作為支撐體系一部分同時承受軸壓力時,其屈曲長度應取為:
Lb,y=KyL,Lb,z=KzL,
其中
Ky=1(或其他分析計算值);
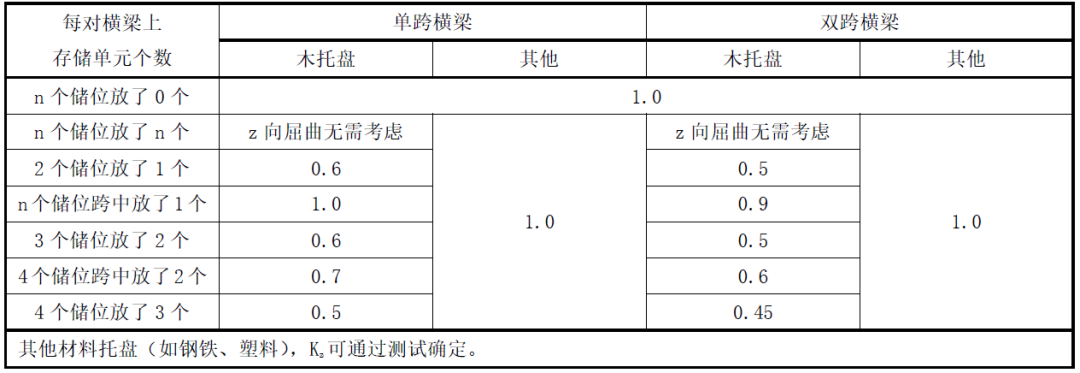
Kz 見表2。
表2 支撐貨架受壓橫梁的屈曲長度系數Kz值
2.6 截面畸變的橫梁
截面畸變的橫梁應通過測試或有限元分析進行設計。
下篇將講述立柱(組)的構件設計。
本站的原創文章,請轉載時務必注明出處:穩圖WESAFE,不尊重原創的行為我們將追究責任。

